Kali ini kita akan membahas logika lanjutan masih dalam materi Diskrit. Matematika Diskrit merupakan salah satu materi wajib bagi mahasiswa yang kuliah di jurusan komputer. Kenapa? ya karena komputer itu sendiri bekerja dengan logika diskrit. Sementara itu judul Logika biasanya dipelajari mulai dari logika dasar, logika lanjutan, hingga aljabar boolean. Setelah sebelumnya kita membahas materi logika, maka kali ini kita akan melanjutkan pembahasan mengenai logika. Jangan lupa untuk dibaca dulu materi logika sebelumnya ya.
Proposisi Bersyarat (Implikasi)
Misalkan p dan q adalah proposisi. Selain dalam bentuk konjungsi, disjungsi, dan negasi, proposisi majemuk juga hadir dalam bentuk “Jika p maka q”. Proposisi majemuk “jika p maka q” disebut proposisi bersyarat (implikasi) dan dilambangkan dengan p->q.
Contoh Implikasi :
- Jika adik lulus ujian, maka ia mendapat hadiah dari ayah
- Jika Ela belajar, maka ia akan pintar
- Jika kamu mendapat nilai ujian di atas 80, maka dosen akan memberikan nilai A
NOTE
Pada Implikasi, p disebut hipotesis/premis/kondisi dan q disebut konklusi/konsekuen.
Implikasi tidak hanya diekspresikan dalam pernyataan standart “Jika p, maka q” tetapi juga dapat diekspresikan dengan cara :
- Jika p, q
- p mengakibatkan q
- q jika p
- p hanya jika q
- p syarat cukup agar q
- q syarat perlu bagi p
- q bilamana p
Tabel Kebenaran Implikasi
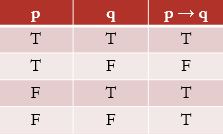
Adapun tabel kebenaran dari Implikasi adalah sebagai berikut :
Implikasi p → q hanya salah jika p benar tetapi q salah
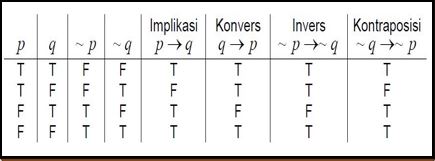
Ada 3 variasi Proposisi Bersyarat :
– Konvers(kebalikan) : q → p
– Invers : ~p → ~q
– Kontraposisi : ~q → ~p
Bikondisional (Bi-Implikasi)
Proposisi bersyarat penting lainnya adalah berbentuk “p jika dan hanya jika q” yang disebut dengan Bi-Implikasi. Bentuk ini adalah bagian dari proposisi bersyarat atau implikasi yang sudah dibahas di atas. Jika dijabarkan, Bi-Implikasi adalah “jika p maka q, dan jika q maka p” artinya dua buah implikasi yaitu dari p ke q dan dari q ke p. Oleh karena itu disebut dengan Bi-Implikasi yang dilambangkan seperti ini p↔q.
Contoh
Jika udara di luar panas, maka anda membeli es krim, dan jika anda membeli es krim maka udara di luar panas.
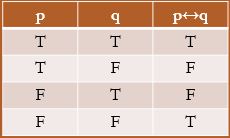
Tabel Kebenaran
Pernyataan p↔q adalah benar bila p dan q mempunyai nilai kebenaran yang sama, yakni p↔q benar jika p dan q keduanya benar atau p dan q keduanya salah.
Bikondisional p↔q ekivalen secara logika dengan (p↔q)^(q↔p) :
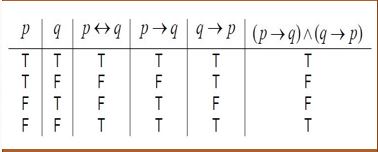
Berikut adalah penjelasan contoh soalnya ya. Semoga dapat memahami dengan baik.
